코딩테스트 하는데 경우의 수 부분이 너무 헷갈려서 정리하려고 따로 포스팅한다.
내가 이 나이 먹고 중2수학 보면서 경우의 수 공부하고 있을 줄은,,
근데 개념을 모르면 다음으로 넘어가질 못하겠는데 어째ㅠ
1. 순열
순열은 원소들의 집합에서 일부 원소를 순서대로 나열하는 방법을 말한다.
이름 그대로 '순서대로 줄을 세운다'라고 이해하면 된다.
순열은 영어로 Permutation이라 첫 글자를 따서 P로 명명한다.
따라서 'n 개 중 r개를 뽑아서 줄을 세운다'는 짧게 nPr로 요약 가능하다.
1) 공식
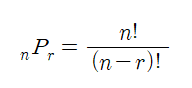
순열의 공식은 위와 같다.
예를 들어, 1부터 10까지의 자연수 중, 2개를 뽑아 일렬로 나열하는 경우의 수를 찾는 문제가 있다.
우선 여기서 숫자 두 개를 각각 {a, b}에 집어넣는다고 가정해 보자.
a에는 1부터 10까지 총 10개의 숫자가 들어갈 수 있다.
그리고 b에는 a에 들어갔던 숫자 하나를 제외한 9개의 숫자가 들어갈 수 있게 된다.
따라서 위 경우의 수는 10*9 = 90이 된다.

이를 공식에 대입해 보면 위와 같다.
2. 중복순열
중복순열은 말 그대로 중복이 포함되어 있는 순열을 의미한다.
1) 공식

중복순열 공식은 위와 같다.
예를 들어, 1부터 10까지의 자연수 중, 2개를 뽑아 일렬로 나열하는 경우의 수를 찾는 문제가 있다고 해보자.
이때 2개의 숫자는 서로 중복이 가능하다.
똑같이 여기서 숫자 두 개를 각각 {a, b}에 집어넣는다고 해보면,
a에는 1부터 10까지 총 10개의 숫자가 들어갈 수 있다.
그리고 b에도 1부터 10까지 총 10개의 숫자가 들어갈 수 있게 된다.
즉 위 문제의 경우의 수는 10*10=100이 되는 것이다.
10*10 = 10^2 이므로 이를 식으로 바꿔보면, n^r이 된다.
3. 조합
조합은 순열과 달리 순서에 상관없이 원소들의 집합에서 일부 원소를 선택하는 것을 의미한다.
'나열'이라는 글자가 들어가면 순열, '뽑는다, 선택한다'라는 글자가 들어가면 조합이라고 생각하면 된다.
1) 공식
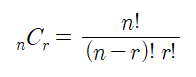
조합의 공식은 위와 같다.
순열에서 r! 를 나눠준 값이라고 생각하면 된다.
순열의 경우 순서가 정해져 있기 때문에 {1,2}와 {2,1}은 다른 값이 된다.
그러나 조합의 경우 순서가 없기 때문에 {1,2}와 {2,1}의 값은 동일하다.
즉, 중복되는 값이 되는 것이다.
따라서 순열에서 해당 값만큼 나눠주면 조합의 경우의 수가 된다.
'Algorithm > 개념' 카테고리의 다른 글
| [2주만에 통과하는 알고리즘] 파이썬 입력과 출력 / 반복문과 조건문 (0) | 2024.03.26 |
|---|---|
| [Algorithm] 깊이우선탐색 알고리즘 (DFS, Depth First Search Algorithm) (0) | 2024.02.04 |
| [Algorithm] 재귀함수 개념과 동작방식 (2) | 2024.01.31 |
| [Algorithm] 이진탐색 알고리즘 (Binary Search Algorithm) (0) | 2024.01.18 |
| [Algorithm] 탐욕 알고리즘 (Greedy Algorithm) (0) | 2024.01.16 |


